This blog post describes the level generator for my puzzle game Linjat. The post is standalone, but might be a bit easier to digest if you play through a few levels. The source code is available; anything discussed below is in src/main.cc.

A rough outline of this post:

• Linjat is a logic game of covering all the numbers and dots on a grid with lines.
• The puzzles are procedurally generated by a combination of a solver, a generator, and an optimizer.
• The solver tries to solve puzzles the way a human would, and assign a score for how interesting a given puzzle is.
• The puzzle generator is designed such that it's easy to change one part of the puzzle (the numbers) and have other parts of the puzzle (the dots) get re-organized such that the puzzle remains solvable.
• A puzzle optimizer repeatedly solves levels and generates new variations from the most interesting ones that have been found so far.

The rules

To understand how the level generator works, you unfortunately must first know the rules of the game. Luckily the rules are very simple. The puzzle consists of a grid containing empty squares, numbers, and dots. Like this:

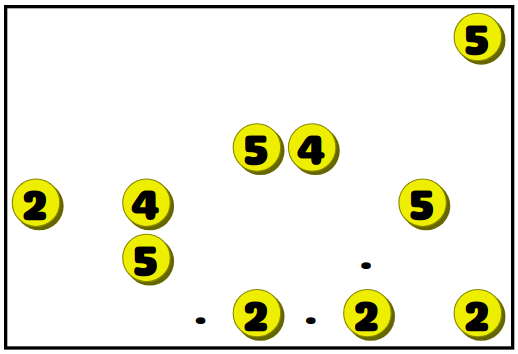
The goal is to draw a vertical or horizontal line through each of the numbers, with three constraints:

• The line going through a number must be of the same length as the number.
• The lines can't cross.
• All the dots need to be covered by a line.

Like this:

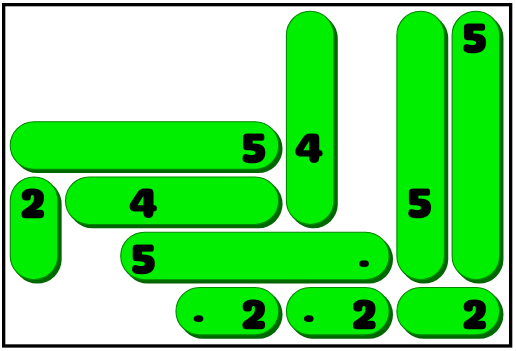
Whee! The game is all designed, the UI is implemented, now all I need are a few hundred good puzzles, and we're good to go. And for a game like this, there's really no point in trying to make those puzzles by hand. That's a job for a computer.

Requirements

What makes for a good puzzle in this game? I tend to think of puzzle games as coming in two categories. There's the ones where you're exploring a complicated state space from the start to the end (something like Sokoban or Rush Hour), and where it might not even obvious exactly what states exist in the game. Then there are ones where all the states are known at the start, and you're slowly whittling the state space down by process of elimination (e.g. Sudoku or Picross). This game is clearly in the latter category.

Now, players have very different expectations for these two different kinds of puzzles. For this latter kind there's a very strong expectation that the puzzle is solvable just with deduction, and that there should never be a need for backtracking / guessing / trial and error. [0] [1]

It's not enough to know if a puzzle can be solved with just logic. In addition to that we need to have some idea of how good the produced puzzles are. Otherwise most of the levels might be just trivial dross. In an ideal world this could also be used for building a smooth progression curve, where the levels get progressively harder as the player progresses through the game.

The solver

The first step to meeting the above requirements is a solver for the game that's optimized for this purpose. A backtracking brute-force solver will be fast and accurate at telling whether the puzzle is solvable, and could also be changed to determine whether the solution is unique. But it can't give any idea of how challenging the puzzle actually is, since that's not how a human would solve these puzzles. The solver needs to imitate humans.

How does a human solve this puzzle? There's a couple of obvious moves, which the tutorial teaches:

• If a dot can only be reached from one number, the line from that number should be extended to cover the dot. Here the dot can only be reached from the three, not the four:

  

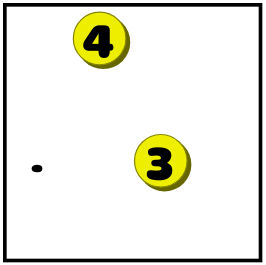
  Leading to:

  

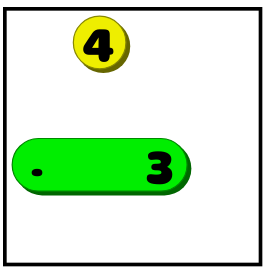
• If the line doesn't fit in one orientation, it must be placed in the other orientation instead. In the above example the 4 can no longer be placed vertically, so we know it has to be horizontal. Like this:

  

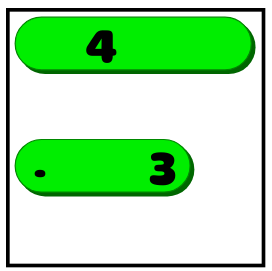
• If a line of size X is known to be in a certain orientation and there isn't enough space to fit a line of X spaces on both sides, some of the squares in the middle must be covered. For example if in the above example the "4" had been a "3" instead, we wouldn't know whether it extended all the way to the right or to the left of the board. But we would know it must cover the two middle squares:

  

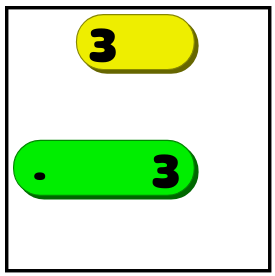
This kind of thinking is the meat and potatoes of the game. You figure a way to extend one line a little bit, make that move, and then inspect the board again since that hopefully gave you the information to make a new deduction elsewhere. Writing a solver that follows these rules would be enough to determine if a human could solve the puzzle without backtracking.

It doesn't really say anything about how hard or interesting the level is though. In addition to the solvability, we need to somehow quantify the difficulty.

The obvious first idea for a scoring function is that a puzzle that takes more moves to finish is the harder one. That's probably a good metric in other games, but in this one the number of valid moves that the player has at any one time is probably more important. If there are 10 possible deductions a player could make, they'll find one of those very quickly. If there's only one valid move, it'll take longer.

So as a first approximation you want the solution tree to be deep and narrow: there's a long dependency chain of moves from start to finish, and at any one time there are only a few ways of moving forward on the chain. [2]

How do you figure out the width and depth of the tree? Just solving the puzzle once and evaluating the produced tree doesn't give a precise answer. The exact order in which you make the moves will end up affecting the shape of the tree. You'd need to look at all the possible solutions, and do something like optimize for the best worst-case. Now, I'm no stranger to brute-forcing puzzle game search graphs, but for this project I wanted a single-pass solver rather than any kind of exhaustive search. Due to the opimization phase, the goal was for the solver runtime to be measured in microseconds rather than seconds.

I decided not to do that. Instead my solver doesn't actually make one move at a time, but solves the puzzle by layers: given a state, find all valid moves that could be made. Then apply all of those moves at once. Finally start over from the new state. The number of layers and the maximum number of moves ever found in a single layer are then used as proxies for the depth and the width of the search tree as a whole.

Here's what the solution for one of the harder puzzles looks like with this model (click on the thumb-nail to expand). Dotted lines are the lines that were extended on that solver layer, solid ones didn't change. Green lines are of the right length, red are not yet complete.

The next problem is that not all moves a player makes are created equal. What was listed at the start of this section is really just common sense. Here's an example of a more complicated deduction rule, which would require some more thought to find. Consider a board like:

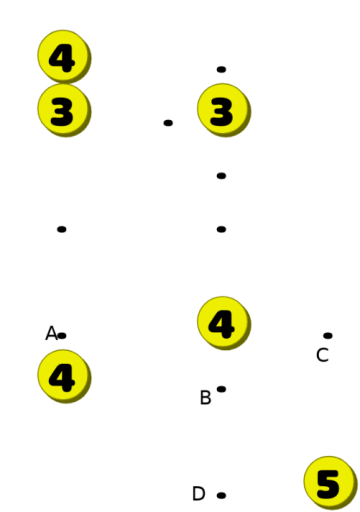
The dots at C and D can only be covered by the 5 and the middle 4 (and neither piece can cover both of them at the same time). This means that the middle 4 needs to cover one of the two, and thus can't be used to cover A. Instead A has to be covered with the lower left 4.

It'd clearly be silly to treat this chain of deductions the same as a one-step "this dot can only be reached from that number". Can these more complex rules just be weighted more heavily in the scoring function? Unfortunately not with the layer-based solver, since it's not guaranteed to find lowest cost solution. It's not just a theoretical concern, in practice it's pretty common for a part of the board to be solvable in either a single complex deduction or a chain of several much simpler moves. The layer-based solver basically finds the shortest path, not the cheapest one, and that can't just be fixed in the scoring function.

The method I ended up using was to change the solver such that each layer consists of only one kind of deduction. The algorithm goes through the deduction rules in a rough order of difficulty. If a rule finds any moves, they're applied and the iteration is over, and the next iteration starts the list over from the beginning.

The solution is then scored by assigning each layer a cost based on the single rule used for it. This is still not guaranteed to find the cheapest solution, but with a good selection of weights it'll at least not find an expensive solution if a cheap solution exists.

It also seems to map out pretty well to how humans solve the puzzle. You look for the gimmes first, and only start thinking hard once there are no easy moves.

The Generator

The previous section took care of figuring out if a level is any good or not. But that alone isn't enough, you also need to somehow generate levels for the solver to score. It's quite unlikely that a randomly generated level would be solvable, let alone interesting.

The key idea (which is by no means novel) is to interleave the solver and the generator. Let's start with a puzzle that's probably unsolvable, consisting just of numbers 2-5 placed in random locations on the grid:

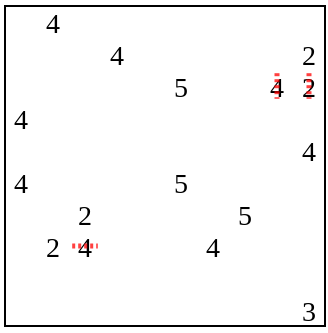
The solver runs until it can't make any more progress:

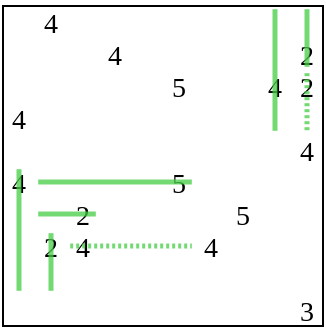
The generator then adds some information to the puzzle, in the form of a dot, and continues solving.

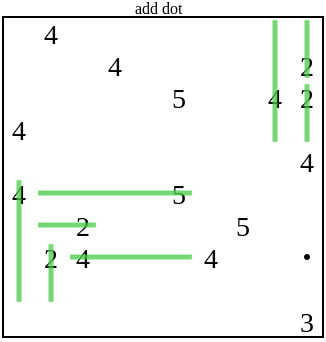
In this case that one added is not enough to allow the solver to make any progress. So the generator will keep on adding more dots until the solver is happy:

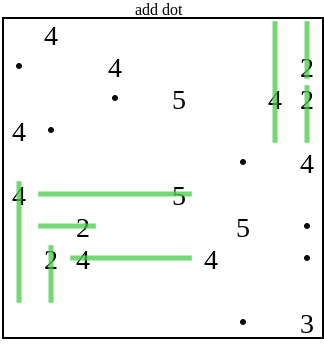
And then the solver resumes normal operation:

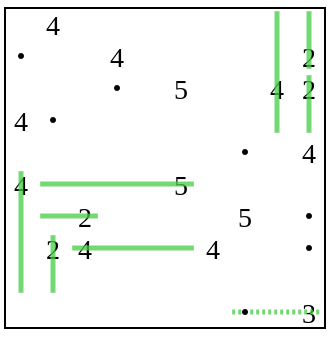
This process continues either until the puzzle is solved or there is no more information to add (i.e. every space that's reachable from a number is covered by a dot).

This method works only if the new information that's being added can't invalidate any of the previously made deductions. That would be tough to do when adding numbers to the grid [3]. But adding new dots to the board has that property, at least given the deduction rules I'm using in this program.

Where shoud the algorithm add the dots? What I ended up doing was to add them in the empty space that could have been covered by the most lines in the starting state, so each dot tends to give as little information as possible. There is no attempt to add it specifically to a location where it'll be useful in advancing the puzzle at the point where the solver got stuck. This produces a pretty neat effect where most of the dots will be totally useless at the start of the puzzle, which makes the puzzle seem harder than it is. There are all these apparent moves you could make, but somehow none of them quite work out. The puzzle generator ends up being a bit of a jerk.

This process will not always produce a solution, but it's pretty fast (on the order of 50-100 microseconds) so it can just be repeated a bunch of times until it generates a level. Unfortunately it'll generally produce a mediocre puzzle. There are too many obvious moves right at the start, the board gets filled in very quickly and the solution tree is quite shallow.

The optimizer

The above process produced a mediocre puzzle. In the final stage, we use that level as a seed for an optimization process. The process works as follows.

The optimizer sets up a pool of up to 10 puzzle variants. The pool is initialized with the newly generated random puzzle. On each iteration, the optimizer selects one puzzle from the pool and mutates it.

The mutation removes all the dots, and then changes the numbers a bit (e.g. reduce/increase the value of a randomly selected number, or move a number to a different location on the grid). It might be possible to apply multiple mutations to board in one go. We then run the solver in the special level-generation mode described in the previous section. This adds enough dots to the puzzle to make it solvable again.

After that, we run the solver again, this time in the normal mode. During this run, the solver keeps track of a) the depth of the solution tree, b) how often each of the various kinds of rules was needed, c) how wide the solution tree was at times. The puzzle is scored based on the above criteria. The scoring function will basically prefer deep and narrow solutions, and at higher difficulty levels also rewards puzzles that require use of one or more of the advanced deduction rules.

The new puzzle is then added to the pool. If the pool ever contains more than 10 puzzles, the worst one is discarded.

This process is repeated a number of times (anything from 10k to 50k iterations seemed to be fine). After that, the version of the puzzle with the highest score is saved into the puzzle's level database. This is what the progress of the best puzzle looks like through one optimization run:

I tried a few other ways of structuring the optimization as well. One version used simulated annealing, the others were genetic algorithms with different crossover operations. None of these performed as well as the naive pool of hill-climbers.

Unique single solution

There's an interesting complication that arises when the puzzle has a single unique solution. Is it valid for the player to assume that's the case, and make deductions based on that? Is it fair for the puzzle generator to assume that the player will do so?

In a post on HN, I mentioned four options for how to deal with this:

• State the "only a single solution" up front, and make the puzzle generator generate levels that require this form of deduction. This sucks, since it'll make the rules far more complicated to understand. And it's also exactly the kind of detail people would forget.
• Don't guarantee a single solution: have potentially multiple solutions, and accept any of them. This doesn't really solve the problem, it just moves it around.
• Punt, and just assume this is a very rare event that won't matter in practice. (This is was the original implementation.)
• Change the puzzle generator such that it doesn't generate puzzles where the knowing the solution is unique helps. (Probably the right thing to do, but also extra work.)

I originally went with the last option, and that was a horrible mistake. It turns out that I'd only considered one way in which the uniqueness of the solution leaks information, and that's indeed pretty rare. But there's others, and one was present in basically every level I'd generated, and often kind of trivialized the solution. So in May 2019 I updated the Hard and Expert mode levels to go with the third option instead.

The most annoying case is the 2 with the dotted line in the following board:

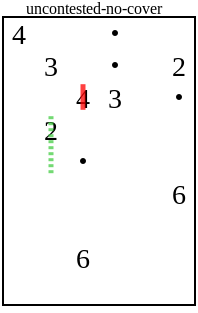
Why could a sneaky player make that deduction? The 2 can cover any of the 4 adjacent squares. None of them have any dots, so they don't necessarily need to be covered by anything. And the square that's downwards doesn't have any overlap with other pieces. If there's a single solution, it has to be the case that other pieces cover the other three squares, and the 2 covers the downwards square.

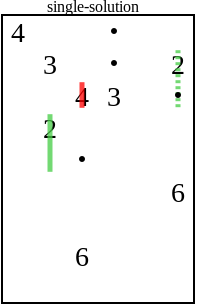
The solution is to add some dots when these cases are detected, like this:

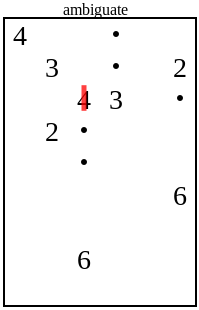
Another common case was the dotted 2 on this board:

Nothing distinguishes the squares to the left and up of the 2. Neither has a dot, and neither is reachable from any other number. Any solution where the 2 covers the upward square would have a matching solution where it covers the leftware square instead, and vice versa. If there's a single unique solution, it can't be either and thus the 2 must cover the downward square instead.

This kind of case I just solved by the "if it hurts, just don't do it" method. I.e. having the solver use this rule very early on in the priority list, and assigning these moves a large negative weight. Puzzles with this kind of property will mostly end up discarded by the optimizer, and the few that make it through will be discarded when doing the final level selection for the published game.

This is not an exhaustive list, I found a lot of other unique-solution rules when adversarially play-testing. But most of them felt like they were rare and difficult enough to find that they're not really shortcuts. If somebody solves a puzzle using that kind of deduction, I'm not going to begrudge them that.

Conclusion

The game was originally designed as an experiment for procedural puzzle generation. The game design and the generator go hand in hand, so the exact techniques won't be directly applicable to existing games.

The part I can't answer is whether putting this much effort into the procedural generation was worth it. The feedback from players has been pretty inconsistent when it comes to the level design. A common theme for positive comments has been about how the puzzles always feel like there's a clever gotcha in there. The most common negative complaint has been that there's not enough of a difficulty gradient in the game.

I have a couple of other puzzle games in an embryonic stage, and felt good enough about this generator that I'd probably at least try similar procedural generation methods for those too. One thing I'd definitely do differently the next time around is to do adversarial playtesting from the start.

Footnotes