Red7 is a very clever little card game, and one of my favorite 2014 releases. But I have wondered about the density of meaningful decisions in the game. Sometimes it doesn't feel like you have all that much agency, and are just hanging on in the game with a single valid move every time it's your turn.
So here's some automated exploration of what a game of Red7 actually looks like from a statistical point of view. The method used here is a pure Monte Carlo simulation, with the players choosing randomly from the set of their valid moves.
Why a Monte Carlo simulation? I started trying to do a full game tree for
a given starting setup but to my surprise the game tree is actually too
large for that to be feasible; 2 weeks of computation even for a
single two player game and a lot of optimization. The branching factor
is just much bigger than it feels like when playing the game.
The rules
(Skip this section if you're already familiar with the game. All you need to know is that we're using the advanced version of the game but without the optional special action rules.)
The rules of the game are very simple. There's a deck of 49 cards (7 colors, numbers 1-7 in each color). In the middle is a discard pile ("canvas"). The color topmost card of the discard pile determines the victory condition. You must be "winning" at the end of each turn you take, or you're out of the game.
There are three options to choose from on your turn. Play a card from your hand to the table in front of you (your "palette"), discard a card from your hand to the canvas, or first play a card and then discard a card. If you discard a card with a number higher than the number of cards in your palette, you get to draw a card.
The winning condition is determined based on the color of the canvas (i.e. top card in discard pile):
| Red | Highest card |
| Orange | Most cards of the same number |
| Yellow | Most cards of the same color |
| Green | Most even cards |
| Blue | Most different colors |
| Indigo | Longest run of sequential numbers (e.g. 4/5/6) |
| Violet | Most cards with a number lower than 4 |
If two players are tied for the winning condition (e.g. the rule is blue and both of them have three even cards in their palette), the winner is the player who had a higher card included in their card combination (cards that didn't contribute to the winning condition are ignored for the tie breaker). This is primarily based on the numeric value of the card. But if two cards have the same value, the one closer to red in the spectrum wins the tie (e.g. green 5 > indigo 5 > green 4).
The implementation
(Ignore this section if you're not interested in the programming, and skip straight on to the results).
I suspect that every Common Lisp program will eventually evolve to using a clever bit-packing of fixnums as its primary data structure. That's the case here as well.
Cards
A card is an integer between 0 and 55 (inclusive). The low 3 bits are the color, with a 0 being a dummy color that's not used for anything, 1 for violet going all the way to 7 for red. The next 3 bits are the card's numeric value minus one (0-6). Note that with this representation determining the higher of two cards is simply a matter of making an integer comparison.
(deftype card () '(mod 56)) (defun card-color (card) (ldb (byte 3 0) card)) (defun card-value (card) (1+ (ash card -3)))
We'll also need a way to represent a set of cards, for a player's hand or palette. We're going to use a 56-bit integer for that, with bit X being 1 if the set contains card X.
(deftype card-set () '(unsigned-byte 56))
Adding and removing cards is simple. (Except how annoying is it that SETF LOGBITP is not specified in the standard?).
(defun remove-card (card card-set) (logandc2 card-set (ash 1 card))) (defun add-card (card card-set) (logior card-set (ash 1 card))) ;; Create a new set from a list of cards. (defun make-card-set (cards) (reduce #'add-card cards))
We'll also need to be able to iterate through all the cards in a set. This is most easily achieved by using INTEGER-LENGTH to find the highest bit currently set, executing the loop body, clearing out the highest bit, and carrying on.
(defmacro do-cards ((card card-set) &body body)
(let ((modified-set (gensym)))
`(loop with ,modified-set of-type card-set = ,card-set
until (zerop ,modified-set)
for ,card = (1- (integer-length ,modified-set))
do (setf ,modified-set (remove-card ,card ,modified-set))
do ,@body)))
Scoring
With these primitives we can then write a very fast function to determine who is currently winning the game. We'll base this evaluation function on scoring a combination of a palette + rule, and comparing the score that each player gets with the current rule. This is a much better way than trying to directly compare the palettes. If you're caching this evaluation function, you get a much higher cache hit rate when the cache key depends only on the state of one player rather than a combined state of two players. (I'm also pretty sure that given this data layout, computing a score will be faster than any kind of direct comparison).
Let's start off with the general structure, and fill in the details as functions under LABELS afterwards. So given a card-set and a color, we'll return a score for that set:
(defun card-set-score (card-set type)
(labels (...)
(ecase type
(7 (red))
(6 (orange))
(5 (yellow))
(4 (green))
(3 (blue))
(2 (indigo))
(1 (violet)))))
Red (highest card) is trivial. We just find the highest card in the set with a call to INTEGER-LENGTH.
(red ()
(integer-length card-set))
For other rules we can make good use of the following helper function. It matches the set against a bitmask, and returns a score based on the number of bits that are set both in the set and the mask (main part of score) which we get with LOGCOUNT, as well as the highest bit set in both (the tiebreaker). Given this definition, most of the scoring types can be written in a very concise manner:
(score-for-mask (mask)
(let ((matching-cards (logand card-set mask)))
(let ((matching-cards (logcount matching-cards))
(best-matching-card (integer-length matching-cards)))
(+ best-matching-card (* 64 matching-cards)))))
For orange (cards of one number) we start with a bitmask that matches all bits corresponding to a card with the value 7. We compute the score for that mask, then shift the mask right by 8 bits such that it covers the cards with the value 6. Repeat 7 times, and find the maximum score. (We don't need to know which iteration produced the highest score, only what the score was).
(orange ()
(loop for mask = #xff000000000000 then (ash mask -8)
repeat 7
maximize (score-for-mask mask)))
Yellow (most cards with the same number) is very similar. We start off with a bitmask that matches all the red cards (so bit 55, 47, 39, etc) and compute the score. Then shift it right by one, such that the mask matches all orange cards instead. Again repeat 7 times and maximize.
(yellow ()
(loop for mask = #x80808080808080 then (ash mask -1)
repeat 7
maximize (score-for-mask mask)))
Green (most even cards) and violet (most cards under 4) are trivial; we can just score a single mask matching the even cards for green, all cards of value 1, 2 or 3 for violet.
(green ()
(score-for-mask #x00ff00ff00ff00))
(violet ()
(score-for-mask #x00000000ffffff))
Blue (most cards of different colors) is where we get into unintuitive territory. Let's start with the tiebreaker; it's obviously guaranteed that he highest card in the palette as a whole can be included in this winning set, so we can just use INTEGER-LENGTH on the whole set the same way we did for the red scoring rule.
To get the number of different colors, we will fold the cardset multiple times. First we'll do a bitwise OR of the high 32 bits and the low 32 bits. Then we'll take OR bits 0-15 of that result with bits 16-31. And finally one more OR of bits 0-7 with 8-15. The low 8 bits are now such that bit 7 is set if any of the "red" bits in the original were set, bit 6 if any of the "orange" bits, etc. We can then just use LOGCOUNT on that byte to get the number of colors present in the palette, and combine it together with the tiebreaker score computed above.
(blue ()
(let* ((palette card-set)
(best-card (integer-length palette)))
(setf palette (logior palette (ash palette -32)))
(setf palette (logior palette (ash palette -16)))
(setf palette (logior palette (ash palette -8)))
(+ best-card
(* 64 (logcount (ldb (byte 8 0) palette))))))
Finally, there's indigo (longest straight). There does not appear to be any clever bit manipulation trick to compute this quickly (if you can think of one, please let me know!). We need to iterate through the cards in order of descending value, ignore any consecutive cards with the same number, and reset our scoring computation when the straight gets interrupted by a missing number.
(indigo ()
(let ((prev nil)
(current-run-score 0)
(best-score 0))
(declare (type (unsigned-byte 16) current-run-score best-score))
(do-cards (card card-set)
(cond ((not prev)
(setf current-run-score card)
(setf prev card))
((= (card-value card) (card-value prev)))
((= (card-value card) (1- (card-value prev)))
(incf current-run-score 64)
(setf prev card))
(t
(setf current-run-score card)
(setf prev card)))
(setf best-score (max best-score current-run-score)))
best-score))
Players
A player is defined as a normal structure, with the only oddity being that they form a circular linked list using the NEXT slot. This tends to be more convenient for iterating through players in turn order than keeping them stored in an external collection of some sort.
(defstruct (player) (id 0 :type (mod 5)) eliminated (hand 0 :type card-set) (palette 0 :type card-set) (score-cache (make-array 16) :type (simple-vector 16)) (next nil :type (or null player)))
The core operation of generating a list of valid moves is deciding whether the player is winning the game after those a move is made. When doing this we'll end up repeatedly evaluating the scores for the same palettes over and over again. To speed this up, there's a minimal cache; for each player / rule combination we store both the last palette we evaluated for that rule, as well as the score.
(defun player-score (player rule)
(declare (type (mod 8) rule))
(let* ((palette (player-palette player))
(cache (player-score-cache player))
(cached-key (aref cache rule)))
(if (eql cached-key palette)
(aref cache (+ rule 8))
(progn
(setf (aref cache rule) palette)
(setf (aref cache (+ rule 8))
(card-set-score palette rule))))))
Given that way to score a player against a rule, we can then check whether the current player is winning the game with the rule.
(defun player-is-winning (player rule)
(loop with orig-player = player
with orig-score of-type fixnum = (card-set-score player rule)
for player = (player-next orig-player) then (player-next player)
until (eql player orig-player)
do (when (>= (the fixnum (player-score player rule))
orig-score)
(return-from player-is-winning nil)))
t)
We can then generate all valid moves by iterating through all the PLAY, PLAY+DISCARD, and DISCARD combinations for the player's current state, and collecting the ones result in the player winning.
(defun valid-moves (player current-rule)
(let (valid-moves)
(labels ((check-discard (play-card)
(do-cards (discard-card (player-hand player))
(unless (or (eql play-card discard-card)
;; Filter out cases where player discards a card
;; without changing rule or gaining a new card.
(and (eql current-rule (card-color discard-card))
(>= (logcount (player-palette player))
(card-value discard-card))))
(when (player-is-winning player (card-color discard-card))
(push (cons (cons :play play-card)
(cons :discard discard-card))
valid-moves)))))
(check-plays ()
(do-cards (play-card (player-hand player))
(setf (player-palette player)
(add-card play-card (player-palette player)))
(when (player-is-winning player current-rule)
(push (cons :play play-card) valid-moves))
(check-discard play-card)
(setf (player-palette player)
(remove-card play-card (player-palette player))))))
(check-plays)
(check-discard nil))
valid-moves))
Other stuff
There's a little bit more code required to generate the scaffolding for a game, and to actually do the random walk through the game tree. None of that code is particularly interesting, nor are the INLINE or TYPE declarations that you'd need to sprinkle on the above code to make it fast. The full code is available on GitHub.
Performance
In the optimal case of trying to iterate through the whole game tree in a 2p game, the average cost of making a move is about 500 cycles, with my desktop doing 7 million moves per second. This is however amortizing the cost of computing the set of valid moves across all of those moves (since in a full search every valid move gets executed). If you're just doing a pure random walk with no backtracking, you'd get no amortization at all. That effect makes an order of magnitude difference.
But it's funny that the biggest profiler hotspot in the program is the PLAYER-SCORE function. Which, if you remember, will simply do an array lookup to get the previous cache key, compare it to the card-set that should be evaluated, and either return a previous result or call out to the real scoring function. The function does basically nothing, but it does nothing really often. When all of the things of substance are pretty fast as well, it's maybe not a surprise that the bottleneck ends up in a place like that.
Results
(Skip this section if you're not actually interested in the game, and just wanted to read some Common Lisp code).
The following results are computed from running simulations of 10k different initial setups, with 100k matches for each simulation with each player making random but valid moves. (So a total of one billion games). All plays were with 3 players, the only player count I consider worth playing.
As a sanity check, I ran a smaller simulation of 1000 initial setups where the players would not play a card + discard, if just playing that same card was sufficient to get into the lead without a discard. The results were very close to the large fully random simulation (e.g. the average game length was 14.6 instead of 14.1 turns, and the win percentage of the best turn order position was 39% rather than 40%).
Finally, an even smaller scale experiment had the AIs use move selection heuristics very similar to those I personally use when playing the game. Those results didn't differ materially from random play either.
Caveats
Unless stated otherwise, all of the numbers are from games with players making completely random moves. It is possible that the aggregate statistics are different when players consciously build toward palettes that are strong in multiple scoring rules, or strong in rules that they have a lot of cards in hand for.
The games are always played with the full deck, rather than in reality as the deck slowly depletes from hand to hand as cards are moved to the scoring piles of players.
Starting player effect
One thing I was curious about is whether the starting player has an advantage, a disadvantage, or neither. It's not obvious, since there are effects both ways.
The case for a disadvantage: Running out of cards means losing the game, and the all other things being equal the first player will also run out of cards first. Due to the way in which the player order is picked, the last player is also guaranteed to have the highest value starting card in their palette giving them a leg up on winning future tiebreakers.
The case for an advantage: The earlier in turn order a player is, the fewer cards the opponents have in their palettes. It's much easier to pass two players with one card each, than two players with two cards each. And this effect continues throughout the game, so it should accumulate over time.
It turns out that at least with undirected random play there's a major disadvantage to being first. It could be that the effect is smaller when players are making "good" moves.
| Position | Win rate |
| 1st | 27.20% |
| 2nd | 32.42% |
| 3rd | 40.37% |
Number of possible moves
Like mentioned above, the branching factor in the game was higher than I'd been expecting. There are cases where players have a lot more moves available than I would have expected.
The theoretical maximum number of options is 7 + 7 + 7 * 6 = 56, where a player can get in the lead either by discarding any of their cards, playing any of their cards, or with a combination of the two. This situation actually happened a total of 483986 times in 14 billion moves (0.03% of the time). A lot more common than I would have thought.
But of course we don't particularly care about the 0.03% case. The more common cases are more interesting. The following graph shows how often you have at least X moves available in the game.
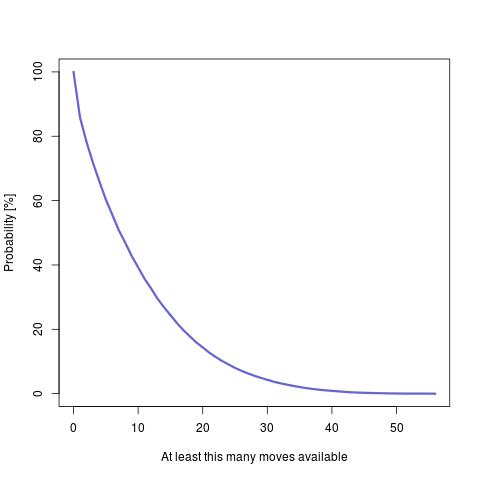
For example, you can see that about a 1/3rd of the time a player had 10 or more options to choose from. It appears that the game is nowhere as constrained as I thought, even when playing without the special action rules.
Length of game
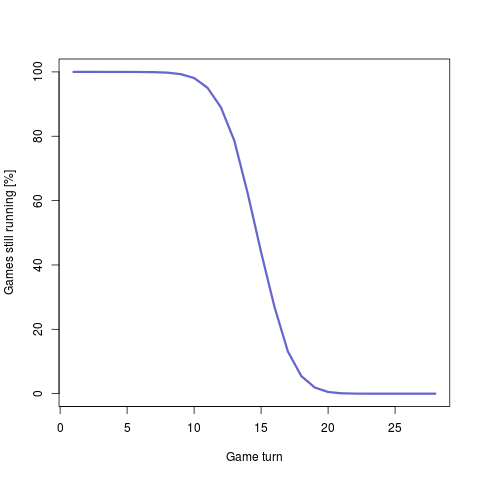
The average game lasted for 14.2 turns, which is perhaps less than I expected given 2 of those 14 turns were by definition a player just dropping out from the match.
There were some games that already ended on turn 4, which meant that only two cards were played in the game. That number was a mercifully low 0.01%. And while there were players who got eliminated before playing a card, there at least were no games ending in turn 2 or 3 even if that's theoretically possible. And a single game lasted all the way to turn 28.
The following graph shows how large a proportion of the games were still running on a given turn.
Effect of player decisions
The final question is about how strongly predetermined a single hand of Red7 is, and how much a player can affect it.
We've already established that at least with this skill level of play there's a very large start player advantage, but is that an isolated issue or does the setup matter even more than that. In these simulations all players are by definition equally skilled. If the end result of the game is primarily determined by player skill, you'd thus expect them to have similar win rates from game to game. So let's graph the distribution of per-setup win rates for each starting position:
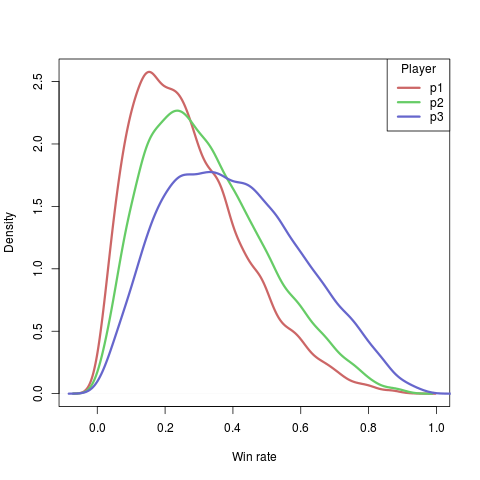
Now, this graph is a little abstract since we're looking at probabilities of probabilities. The way to read this is that across those 10000 starting setups, the most common win percentage for player 1 (red) across the 100000 games in a specific setup was around 15% (the peak of the red line is at around 0.15). You can see that the later players in turn order have a graph that's shifted further to the right, which is what you'd expect when they have a substantially higher win percentage. But you can also see that from any starting position you might get absolutely dismal win rates (near 0) or very high win rates (over 80%). The ridiculously high win rates (95%) appear to be purely reserved for the player last in turn order.
There were two setups where a player didn't manage to win even a single match out of 100000 (in both cases that was player 1). In 25% of the cases the player with the worst chance of winning a setup had a 10% win rate or lower, in 7% of the cases a win rate of 5% or lower. It does appear that within a single hand of Red7, luck plays a massive role.
Out of all of the questions we've been looking at, this is of course the one where the applicability of a purely random search strategy is the most questionable. If we're investigating the effect of player skill, how can results from the least skillful play imaginable be relevant? I'm sympathetic to that argument, but before buying into it I'd really like to understand the mechanism by which one player is supposed to disproportionately benefit from the random play.
Also... As mentioned earlier, I also tried extending the AIs to be smarter about selecting each move. This was not based on any kind of lookahead, but simply the kinds of heuristics I'd usually use myself when playing the game. If I can get into the lead either by playing a card or discarding a card (without drawing a new one to replace it), I'd rather play a card since that's going to be useful on future rounds. When choosing which of two cards to play, I'd usually prefer to play the one that adds strength to more different scoring rules.
Experiments with one AI player getting use of these kinds of heuristics while the others played completely randomly did not show a big effect, the changes in the win rate were on the order of 1-2 percentage points.
Future work
I might be done with this little project, but if I pick it up again there's a couple of obvious directions to take this. Implementing the optional special action rules would be nice. That's my preferred form of the game anyway.
The more interesting one is to extend the current system to be a full AI using the Monte Carlo Tree Search approach. This would allow generating statistics based on "good" play of the game, maybe provide information on what kinds of moves are in general successful, as well as give a more conclusive answer to the level of skill the game has.
The tricky bit with evolving this code to a MCTS is that the system in the current form would allow the MCTS to exploit knowledge of future random events and hidden information. It would need to randomize all card draws (currently deterministic), as well as swap the opponents hands for random cards for the duration of the evaluation phase, and then swap the original deck and original hands back in for the move execution. That's going to slow down each individual move a lot, which is a problem when MCTS will intrinsically require computing several orders of magnitude more moves than a random walk.
I suspect the answer to this will be obvious to anyone who's played red7, but I haven't played red7. Is the game random enough that a random player could beat an experienced player?
I have a vague recollection of someone doing that analysis for fluxx. The "AI" player would take any action that would cause an immediate win. Otherwise, they played randomly. IIRC, the "AI" won about 35% of the time, which led them to conclude that fluxx is not very random.
35% is lower than the 50% you'd get in the war card game, but if you tried that algorithm in a game that's considered to have a large element of randomness that isn't almost totally random, like dominion or tichu, the win rate would be so close to 0% that I doubt you'd ever see an "AI" win.
Which category does red7 fall into? Is it in war/fluxx territory, or closer to dominion?